Summary
In this article, we overview the risk assessment analytics and management process and explore the notions of robustness and resilience as complementary analytical tools in dealing with uncertainty.

Take Our Content to Go
It is critical for an enterprise to identify the obstacles that could compromise its ability to deliver and ensure that appropriate responses are in place. In risk management language, it is all about identifying the organization’s threats and vulnerabilities, understanding their impact, and implementing controls to ensure that they do not significantly compromise operations. This involves being cognizant of the risk factors inherent in the organization’s capabilities and ensuring true robustness and resilience through effective risk management techniques across the entire ecosystem for a broad diversity of risk factors.
In this article, we overview the risk assessment analytics and management process and explore the notions of robustness and resilience as complementary tools in dealing with uncertainty. We also offer insights into the roles that Simulation, Mathematical Optimization (MO), and Machine Learning (ML) play in this context.
The Risk Assessment Analytics and Management Approach
Many organizations practice risk assessment analytics techniques to cope with uncertainty and manage undesirable outcomes. The motivation for this may come from external sources, like regulations and laws that impose some sort of action to ensure a certain operational safety. But it also stems from within, especially in mature organizations concerned with topics like continuity of operations in emergencies and natural disasters or the cascading effects that changes in international markets or supply chains can have on the public sector or private companies.
Assessing Risks
The risk assessment analytics process varies in the terminology, scope, and tools used to perform the analysis across sectors, but overall, it follows the same guiding principles, masterfully summarized by S. Kaplan and B.J. Garrick’s three questions1: 1) What can go wrong? 2) How likely is it to go wrong? and 3) If it does go wrong, what are the consequences?
In practice, however, answering these questions may prove very challenging. Key to a successful risk assessment analytics exercise is a correct definition of the scope of the analysis, namely, what (sub) system is under focus, its mission and performance metrics, as well as all upstream and downstream flows and interdependencies associated with the system. Once there is clarity about these aspects, the analysts can move on to approach the three questions on solid footing.
Scenario identification requires a good dose of creative thinking, but most importantly, it relies on a thorough understanding of how the system operates. Besides, the more a system is intricately interconnected with others, the more difficult it becomes to anticipate trickle-down and systemic effects.
Many techniques have been devised over the years to help identify adverse scenarios in risk assessment. Classic methodologies such as HAZOP, FMEA, FTA, etc. (see Box 1), are widely used in industrial sectors for engineered systems. In less technical environments, approaches such as rounds of expert elicitation are commonly applied. In both cases, the goal is to exploit subject matter expertise and historical records in a systematic way to help generate good amounts of insights into what can go wrong.
BOX 1: THE TOOLS OF RELIABILITY AND RISK ANALYSIS
- FMEA: Fault Modes and Effect Analysis
- FMECA: Failure mode effects and criticality analysis
- FTA: Fault Tree Analysis
- ETA: Event Tree Analysis
- ESD: Event Sequence Diagram
- HAZOP: Hazar and Operability Study
- RBD: Reliability Block Diagram
The next steps in the process are the estimation of likelihoods and consequences. Some of the techniques mentioned above are useful in helping answer questions 2 and 3 both from a qualitative and a quantitative standpoint. In the first case, categorical statements such as “this scenario has low likelihood but high consequences” are valid ways of discussing risk that can be accommodated in a risk matrix. However, it is not difficult to see how a process based on having experts identify scenarios and attach likelihood and consequence labels to them may quickly become intractable unless the number of scenarios is small. This is further aggravated by the inherent limitations of comparing things with the same label. For example, if scenarios A and B both have low likelihood and medium consequences, does it mean that both are equivalent in terms of risk? Are the likelihoods equally “low” and the consequences equally “medium” for both scenarios?
BOX 2: MAIN QUANTITATIVE APPROACHES USED IN PROBABILISTIC RISK ANALYTICS
- Simulation: the construction of alternate realities from mathematical and computational models to perform experiments and explore system behavior under different conditions. The model can be very simplistic approaches to reality or complicated digital twins that account for many systemic variables and relationships (see Box 3). The versatility of simulations makes them a great ally for analysts seeking to generate and test many what-if scenarios. Nonetheless, it is important to remember that a simulation is as good as the models and set of assumptions underpin it. Hence, they are not immune to producing inadequate, incomplete, and even wrong results.
- Data-Driven Models: when enough data is available, a large catalog of Machine Learning models is available to analysts to generate system outcome predictions. These types of models have the advantage that they can learn complicated relationships directly from the data, thereby reducing the effort that analysts must invest in understanding and modeling the system.
- Hybrid Approaches: a third category seeks to exploit the strengths of each modeling technique to produce an even more powerful tool. This can be achieved, for example, by embedding machine learning models within the simulation where otherwise would be fixed sets of rules or fully specified mathematical or statistical expressions. Another alternative is using simulations to generate examples for data-intensive machine learning models like deep neural networks.
Quantitative assessments quickly solve some of the issues we just mentioned. When likelihood is expressed as probabilities, we now have a numerical dimension that makes comparisons straightforward. Consequence estimation is also much simpler, given that all consequences are on the same scale. Admittedly, this is not always easy, especially when we deal with multidimensional consequences. Yet, methodologies like assigning every dimension an equivalent dollar value or performing analyses in multidimensional spaces can help here.
At any rate, quantitative assessments are the basis for Probabilistic Risk Assessment and constitute the preferred way of conducting risk assessment analytics among specialists, not only due to the inherent advantages of using numeric scales over categorical values but also because they broaden the range of tools that can be used to characterize likelihoods and consequences. The main categories of such tools are described in Box 2. One of them, namely simulation, is further developed in Box 3.
BOX 3: SIMULATION TECHNIQUES USED IN RISK ASSESSMENT ANALYTICS
- Process Simulation: the representation of a chemical, physical or biological process using a computer model to predict its response to different inputs and parameters.
- System Dynamics Simulation: a dynamic model based on feedback loops and differential equations used to simulate the evolution of a system over time as an aggregate, i.e., from a high level of abstraction. The Susceptible/Infected/Recovered (SIR) epidemiological model is a well-known example of this category of simulations.
- Discrete-Event Simulation: based on intermediate levels of abstraction, this approach discretizes time as a sequence of steps while seeing the world as a process comprising different interrelated entities. At each time step, each entity can have only one state out of a discrete list of allowable states. An event is a change in the current state, which can happen randomly or be triggered by other, interconnected entities upstream.
- Agent-Based Simulation: this approach allows for the modeling of system elements as separate entities with their own behavior and rules to interact with other entities. Agents can represent many things (e.g., people, vehicles, animals, containers, computer servers), and different classes of agents can take part in a simulation. This is useful, for example, to study emergent behaviors in complex systems or to study how particular individuals engage with highly complex environments.
- Monte Carlo Simulation: is a way of estimating values or probability distributions by multiple repetitions of an experiment involving a system that already contains random variables or a problem that is susceptible to being solved using introducing a random variable.
Quantifying Risks
The next step in the process is quantifying risks from their individual components. A common approach among risk analysis practitioners is to quantify risks as R = P x Q (Eq. 1), where R stands for risk, P is the scenario’s probability of occurrence, and Q its consequences. One property of Eq. 1 is that it allows for two different scenarios to have the same risk value; this is called iso-risk.
Sometimes the public perception prevents Eq. 1 from being used because some consequences are not considered additive. Consider, for example, a first scenario of multiple fatal traffic accidents with an overall death toll of 100 drivers versus another scenario where 100 passengers die in one airplane crash. Obviously, the raw consequence is the same in both cases, but experience shows that the latter has a much greater impact on society. This phenomenon is known as social amplification of risk, as is modeled by adjusting the consequence with a factor n ≥ 1, thus yielding R = P x Qn(Eq. 2).
Equations 1 and 2 are not the only ways of quantifying risks. Another equation popularized by the US Department of Homeland Security is R = T x V x C (Eq. 3), where T stands for threat, V for vulnerability, and C for consequences. While in Eq. 1, something like “probability of structural collapse caused by earthquake” is captured by P, in Eq. 3, these aspects are decoupled: T represents the probability of earthquake and V probability of collapse given that an earthquake happened. Those familiar with statistics quickly recognize in V a conditional probability. C is conditional too. By contrast, T may or may not be independent, depending on whether the scenario is one of a random origin or an intentional event.
It may seem that the factors in equations 1 to 3 are numbers, but this need not be the case. Any one of those factors could be replaced by a distribution. In the previous paragraph, for example, the probability of an earthquake is better represented by a probability distribution than a fixed number.
Moreover, earthquakes vary in magnitude, so T could be the probability of an earthquake of a given magnitude in the next y years. Likewise, V may be expressed as the probability of sustaining a certain amount of damage given that an earthquake of some magnitude happened. A similar idea applies to C. Resorting to simulation to generate scenarios or assess consequences may be one of the reasons for using distributions in the risk assessment analytics calculation. Also, some models like the likelihood of occurrence of natural disasters are probability distributions.
Finally, notice that whenever we stop using numbers in favor of distributions in at least one of the factors of the risk assessment analytics calculation, the result becomes a distribution too. When this happens, the risk could be communicated in certain quantiles or exceedance probability.
Managing Risks
Once the risks have been properly identified and characterized, it is time for the responsible parties to decide how to cope with them. Risk management strategies are domain-specific, but in general terms, they fall into one of these four main categories, namely Risk Avoidance, Risk Acceptance and Sharing, Risk Mitigation, and Risk Transfer.
The first category refers to performing actions to remove certain risks, for example, by ensuring that some scenarios never happen. Eq. 3 could mean eliminating sources of threat (e.g., by detection and deterrence) or reducing the system’s vulnerability (e.g., with structural reinforcements in the case of infrastructures).
In the second category, the responsible parties are willing to bear the consequences should any scenarios happen. Sometimes other entities like parent companies or government agencies are willing to assume part of the consequences hence “sharing” the risks.
The third category corresponds to the deployment of systems and protocols to contain adverse scenarios from fully unfolding. Instances of risk mitigation measures are abundant in our daily lives: safety belts, computer antiviruses, and firefighter stations are just a few examples. Lastly, risk transfer happens when an external party, typically an insurance company, absorbs the risk, in a partial way and under certain conditions, on behalf of responsible parties.
Risk Management as a Mathematical Optimization Problem
Beyond the steps that may be codified in the applicable laws and regulations and some recommended best practices stemming from professional committees and other concerted efforts concerned with risk reduction in different sectors, there is, in general, no specific recipe to manage risks. Instead, risk management efforts can be approached as a portfolio optimization problem.
Let us consider risk as expressed by Eq. 3. Assume there is a set of different measures that a decision maker can implement to bring down risk; some can help reduce the threat likelihood T, others can contribute to reducing the system’s susceptibility V, while others mitigate the consequences C. It is conceivable that the same measure can exhibit different performance levels under different scenarios.
Let x represents a specific configuration of risk assessment analytics management measures from the set of portfolios X, and cost(x) is its monetary cost. We can model risk for scenario s as R(x,s) = T(x,s) x V(x,s) x C(x,s) (Eq. 4), where the right-hand side terms account for the impact of implementing x over the threat, vulnerability, and consequence of scenario s. In general, a condition for a good portfolio x is that it has a non-incremental value on the factors of Eq. 4 across all scenarios (i.e., T(x,s) ≤ T(s) ; V(x,s) ≤ V(s) ; C(x,s) ≤ C(s) for all instances of s)
In various scenarios, each portfolio gets not one but many measures of risk. For example, given two scenarios s1 , s2 and two portfolios x1 , x2, Eq.4 yields the following combinations: R(x1,s1) , R(x2,s1) , R(x1,s2) , R(x2,s2). To decide whether x1 performs better than x2 in risk, decision-makers need to adopt some criteria to handle multidimensional comparisons. Often this amounts to producing one representative value for each portfolio, such as a quantile or the average. Once these criteria for comparison are settled, we are in a position to tackle the problem from a mathematical optimization angle.
Let us assume we decided to compare portfolios using the maximum risk across all scenarios. The optimization problem can have different formulations:
1. We can try to minimize maximum risk within a fixed budget:
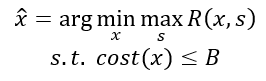
2. We can try to minimize costs while bounding risks:
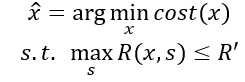
3. Or we can try to minimize both:
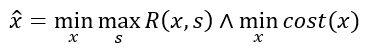
All these formulations constitute valid mathematical optimization programs that help decision-makers find the best portfolios to manage risks. In practice, they might report different results due to what is being constrained in Eq. 5 (budget) versus Eq. 6 (risk). Moreover, Eq. 7 is likely to report multiple solutions, known as efficient or non-dominated by practitioners, representing the set of portfolios whose cost cannot be further decreased without increasing risk.
Alternative Ways of Approaching Uncertainty
In this section, we introduce the concepts of robustness and resilience and discuss ways to quantify them. The reader may notice some conceptual overlap among these ideas. Indeed, they all highlight different parts of the spectrum of ways in which we can cope with uncertainty.
Robustness
In common speech, we say something is “robust” when it withstands different environmental conditions and performs well under various usage regimes without much degradation. A similar notion exists for engineered systems, where robustness signifies the range of conditions under which a system is designed to operate (e.g., waterproof electronics are more robust since they operate well in dry and wet environments) as well as the ability to withstand deviations from those conditions without losing function.
Since it is impossible to anticipate how a system will be utilized, to make it more robust, the designer has an effective strategy to account for the uncertainty in the usage patterns and environmental conditions such system will be exposed to. Moreover, robustness need not circumscribe objects, like cars or buildings, but can also be predicated on intangible things, like supply chains or travel plans. In this case, the ability to absorb delays while meeting goals becomes a marker of robustness.
An important question to consider is how robustness can be quantified. As we saw with risk, robustness can also be operationalized differently. We already alluded to waterproof electronics being able to work under dry and wet conditions (two scenarios), as opposed to dry environments only (one scenario). In this simple example, the number of scenarios indicates how robust the electronics are. We can generalize this by quantifying robustness in terms of size or cardinality.
Let x represent a potential solution in a design space X, and s be the usage scenario. Let I(x,s) be an indicator function that returns 1 if solution x performs well under s and 0 otherwise. We can quantify the robustness of x as Ro(x) = ΣS I(x,s) (Eq. 8), i.e., the number of scenarios where x performs.
The binary nature of the indicator function suggests that some sort of hard constraint is needed in its definition. The most obvious case for I is to become a function/no function indicator, but it could also work with performance thresholds, such as returning 1 if the loss of service level < 15% and 0 otherwise.
We can measure interval sizes to quantify robustness when dealing with continuous dimensions like temperature or time rather than counting scenarios. For example, in scheduling, the goal is to assign a set of tasks start times while reducing the total duration or makespan. The problem is often accompanied by logical constraints that have to do with precedence rules or resource-sharing limitations.
Since start times and task durations are subject to uncertainty in real life, each potential schedule can be assigned a robustness measure built around the size of the intervals. Figure 1 depicts three possible ways of sequencing tasks A, B, and C within an execution window demarcated by the earliest acceptable start and maximum acceptable completion times.
Notice that the green schedule has the smallest makespan of the three but at the expense of leaving very little margin for absorbing delays. The other two schedules are more robust and have very similar makespan, but while delays in the completion of task B can be easily handled in both schedules, the orange schedule surpasses the blue one in its ability to absorb delays in task A. In practice, instead of the visual analysis we did, one can measure robustness as the minimal size of the time interval between consecutive tasks. Alternatively, robustness can be estimated as the product of all interval sizes.
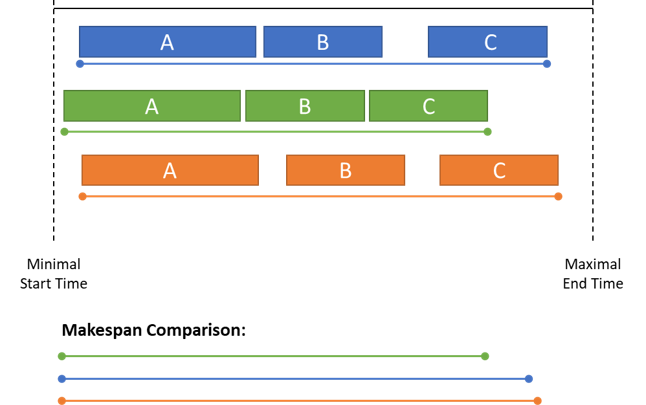
Finally, it may be evident, but it is worth reiterating that robustness has a cost. The loss of optimality in makespan seen by the blue and orange schedules in our previous example is paradigmatic of robust solutions. This is explained by the fact that robustness is inherently concerned with performing well in a larger multiplicity of scenarios than the standard case. This does not mean, however, that a robust design or solutions are condemned to be markedly suboptimal, either in performance metrics or monetary cost. Instead, some robustness level can be prescribed as a constrain while the performance metric P is optimized, yielding
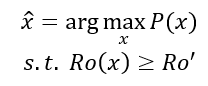
Alternatively, both robustness and performance can be improved simultaneously in a multiobjective formulation:
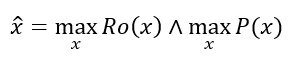
Resilience
The concept of risk focuses on one important aspect of coping with uncertainty: anticipating unwanted scenarios and preparing for them. On the other hand, robustness stresses the ability to absorb or withstand such scenarios while minimizing loss of performance. One can say that these two aspects are primarily oriented towards preparation and avoidance. However, when an unwanted event happened, the system of interest must be restored or replaced by something different. The ability to resist, adapt, and perform in the aftermath of an event is known as resilience.
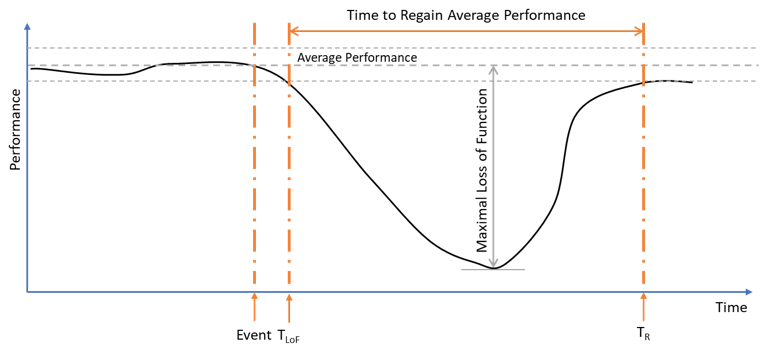
Figure 2 exemplifies how the system performance may change over time with the occurrence of an unwanted event. This period of disruption is characterized by a performance dip or valley below the average performance range, whose length TR – TLoF is the time to regain pre-event performance and whose depth indicates the maximum loss of function or output experienced by the system.
Ideally, we expect the system to be able to go back to its pre-event state as quickly as possible. In other words, we want the valley’s depth and length to be minimal. In practice, this is not always possible. Indeed, sometimes the system cannot return to its previous state, either because it was impacted in some unrepairable ways or because the external conditions change.
An example of the former is when a natural disaster damages some infrastructure to the point where it must be torn down and reconstructed. In such cases, there might be room for some adaptation and ingenuity, but at the same time, the cost of repairing the system may prevent it to be rebuilt. Concerning the latter case, consider a retailer that suffers some disruption in its supply chain, unwillingly forcing its customers to purchase from its competitors; in some cases, the loss of customers may be permanent even if the system can return to its former stock levels and variety.
Stakeholders concerned with making the system more resilient can consider different strategies. The exact nature of what to do depends heavily on the nature of the system, so we are not going to consider specific examples. Redundancies, backup reservoirs, contingency plans, etc., are common resilience-improving strategies.
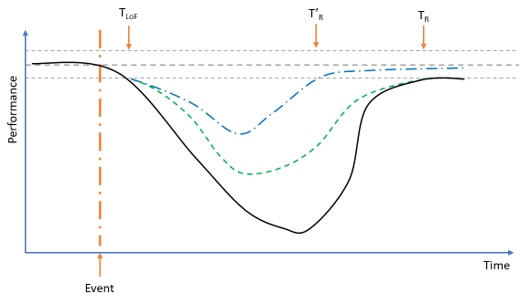
Fig. 3 illustrates the effects that risk assessment analytics for improving resilience may have upon the system performance profile shown in Fig. 2. One possible outcome may be a reduction in the amount of output loss without impacting the time to recover function TR (green profile). The other preferable outcome in blue exhibits a reduction in time and depth.
While in practice, it is not possible to know a priori the actual shape of the curve, past experiences and the use of simulations may shed some light on how the journey to recovery may look like. Obviously, the answer may be in the form of an interval or distribution of plausible recovery profiles rather than a crisp forecast. Nonetheless, decision-makers can then use these results, even if they are approximate, to inform their decisions regarding preparation and response strategies and resource and budget allocations. Once again, mathematical optimization can play a role here in the same fashion we saw before.
Conclusions
This article reviewed the notions of risk, robustness, and resilience. We showed how to frame these concepts within an optimization problem to equip stakeholders with effective tools to cope with uncertainty. Our intention has been to paint a big picture only, so we purposely have excluded many conceptual and practical nuances and kept hidden some of the big complexities involved in modeling the problem, deploying a simulation, or optimizing the allocation of resources in the presence of uncertainty.
Are you confident that your risk assessment analytics strategy is sound? Do you worry that there are risk factors that you are missing during the assessment and analysis phases of risk management? At Mosaic, we have a team of experts that can assist with deploying these strategies to help you get up to speed on any lurking risks and find ways to prevent and mitigate them.
Endnotes
- Kaplan, Stanley, and B. John Garrick (1981) “On The Quantitative Definition of Risk”, Risk Analysis, vol. 1, pp.11-27


