Summary
How machine learning and mathematical optimization can be combined to solve problems more effectively.

Take Our Content to Go
Introduction
Throughout history, humankind has invented tools to help solve complex problems. Indeed, the common Neanderthal’s resume 100,000 years ago may have begun with “I excel at leveraging tools and technology to help my tribe solve complex problems.” We’ve always loved our tools. One could argue that it’s a defining characteristic of humans. However, some form of human bias often leads us to over-extend the usefulness of the tools we know into problem domains where they don’t fit. Perhaps we’ve been doing this since our caveman friend was around.
There are times when it is helpful to level set on the best applications of the tools we’ve invented and identify how these tools can be combined to solve problems together. Instead of either/or, why not both? In this whitepaper, we at Mosaic explore how two transformational technologies can be brought together to help organizations solve their problems more effectively. This whitepaper dives into the integration of Machine Learning (ML) and Mathematical Optimization (MO).
The Elephant in the Room
Before we get into the details, let’s clear the air a bit. For many of those reading this blog post, you probably have a good sense of what ML is and perhaps little idea as to what MO is. In short, while ML is focused on solving prediction problems (e.g., what is going to happen next or how you would classify an object), MO, at least within the context of Operations Research, is focused on solving big decision problems (e.g., given 10 million possible choices, what is the best series of decisions to make?).
For the past several years, ML has exploded in popularity, while the excitement for MO has mostly plateaued. Why this has occurred is very much up for debate. One might surmise that ML is simply a better tool than MO, and therefore it replaced it in terms of popularity. This, however, is wrong-headed. ML and MO are typically used to solve very different problems. One might also think that problems MO has historically solved no longer exist. This, too, is a reduction. Scheduling, routing, assignment, and other major decision problems are more pervasive than ever. The reasons for the rise in popularity of ML coinciding with the fall in favor of MO are more nuanced. While indeed not a complete analysis, here are just two example factors that demonstrate how nuanced the situation is:
- We’ve already tackled the most pervasive and challenging optimization problems in our society. Amazon has figured out how to do free two-day shipping. Airlines have figured out how to create schedules with minimal delays, and manufacturers worldwide have figured out how to minimize the cost to provide affordable products. Not to say that the models driving these decisions can’t be improved, but they have at least mainly been tackled. This has created less excitement and research for large-scale optimization (this will happen to ML, too, by the way). In short, the peak of the hype curve for optimization is already behind us.
- At optimization’s peak, companies like Amazon, Google, Microsoft, etc., were not evangelizing math-intensive technologies during Super Bowl ads. These tech companies have many relatively novel prediction problems to solve (e.g., facial recognition, image classification, natural language processing). So it’s no surprise that much of their R&D and marketing efforts are so focused on ML. That’s not to say that these companies aren’t running substantial optimization models to make their most critical operational level decisions. It’s just not where the excitement is at right now.
ML’s rise and MO’s plateau have led to some tension in the world of Operations Research. One might say there is some jealousy right now at how popularized ML has become. People in the MO world treat ML as all hype, while people in the ML world treat MO as archaic. However, these discussions are trivial. MO had its hype cycle, and traditional ML algorithms are already being viewed as ancient by some.
At Mosaic, we care about identifying the right tool for the right job, meaning that the relative popularity of the technologies we leverage is a moot point. After all, math itself is a few thousand years old. So, in the spirit of dedicating the use of tools to solve problems, instead of using problems to demonstrate the efficacy tools, we propose an exploration of how ML and MO can complement each other in solving problems.
The Case for Mathematical Optimization
As mentioned previously, mathematical optimization techniques are charged with finding the best possible set of decisions to make in a given scenario. Instead of making predictions, its task is to recommend actions. While small problems can often be solved by just trying every possible option, most problems quickly explode in size to the point where it is computationally impossible to evaluate every possibility. A typical optimization model is given below.

Shown graphically:
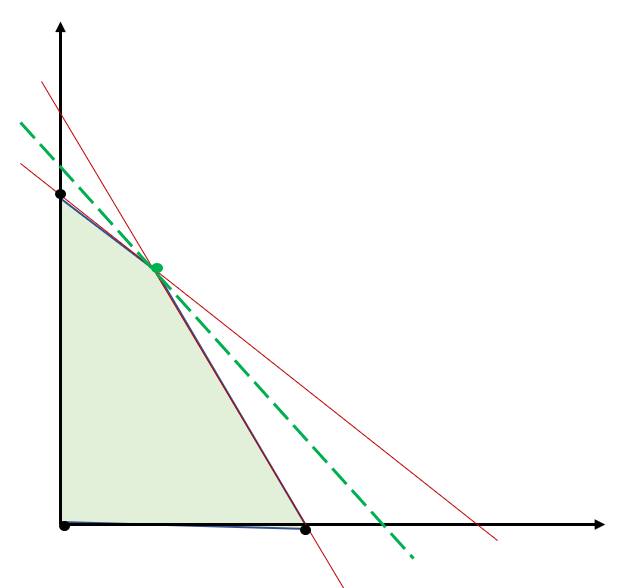
Here the goal is to find decisions (x) that maximize or minimize the value of the objective function, all while abiding by the underlying constraints. Graphically, in a two-variable problem, we are trying to find the set of (X, Y) coordinates that maximize the value of the green dotted line while remaining within the feasible region (shaded area). Algorithms in this space typically use linear algebra to solve the set of equations to optimality.
Mathematical optimization excels at finding optimal solutions to big decision problems without trying out every combination of possible decisions. This approach is beneficial for solving problems in various domains, including scheduling, resource assignment, routing, and many others. However, like every tool, it is not a magic bullet. As is typical with technology, there are a few common challenges with using MO to solve problems. First, MO algorithms can be slow when the solution space is vast, and optimality is required. Second, many optimization problems can be very tricky to formulate mathematically. Third, and the challenge most critical to this discussion: traditional optimization techniques are deterministic. This means the same set of inputs to a model will generate the same output. Inputs are assumed to be known. This presents a problem that traditional optimization cannot answer by itself: What do we do if some of the model inputs are not known with 100% certainty? Some inputs are just a matter of fact (e.g., you have a fixed budget). There is no randomness, no uncertainty in their values. However, the world is a very uncertain place, and for the output of optimization models to be valuable, we need to address this question of uncertainty.
One approach that can be useful is to integrate simulation into the optimization process. With this approach, input values are simulated and passed through the optimization model, each time generating a different optimal solution. Integrating simulation with optimization can be helpful, especially when one wants to gain higher-level insights into optimal behavior in an uncertain environment. However, this is not always the best approach. Very often, operational-level decision-making requires algorithms to return solutions quickly. Wrapping a simulator around an optimization model can be very computationally expensive. The optimization alone might take minutes to run, so running thousands of iterations either requires heavy computation, parallelization or a lot of patience. Therefore many problems require an alternative approach to the problem of uncertainty.
The Case for Machine Learning
While mathematical optimization takes a deterministic approach to recommend the best actions, machine learning algorithms typically take a statistical approach to make predictions. ML excels at tackling the prediction problems that naturally fall under two broad categories: classification (predicting a label) and regression (predicting a quantity). Given regression problems are going to be more relevant for this discussion, below is the structure of a simple linear regression problem:
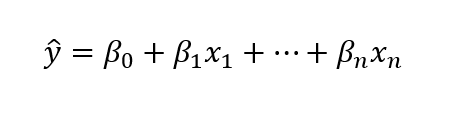
Shown graphically:
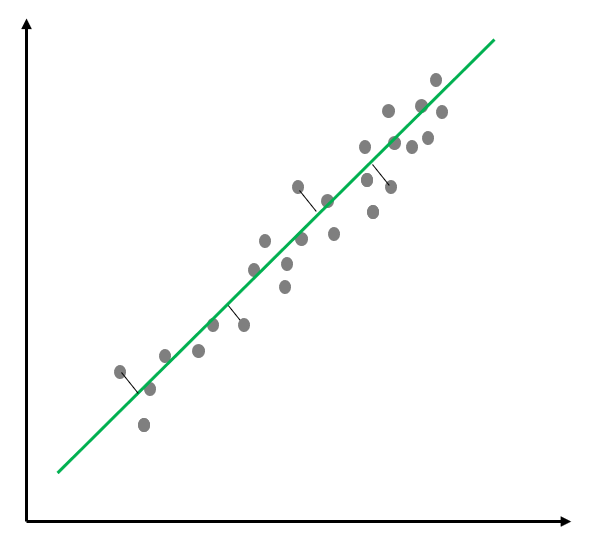
The goal of regression is to find parameters (β) that minimize the loss or error. Graphically, we are trying to define a line that is as close as possible to the observed data. Indeed, the goal of any ML algorithm is to minimize some loss function. Sound familiar? That’s right: ML problems are just MO problems with a funny hat on. In both MO and ML, the goal is always to optimize the value of some function. The critical differences between ML and MO are in the methods used to solve and the problem domains they are best suited for. As a review, ML algorithms typically take a statistical approach and are best at solving prediction problems. In contrast, MO algorithms typically use linear algebra and are best suited for decision problems.
ML techniques also come with several challenges. First, ML algorithms typically require lots of training data to develop accurate models. Second, they are prone to overfitting (memorization) and over-generalizing patterns in the data. Third and most important to this discussion: predictions alone often fall short of what decision-makers need to make complex decisions. The projections that ML algorithms make often beg a follow-up question: “okay, so what should I do?”. To give a simple example, an ML model that predicts a stock price begs the question of whether or not you should buy the stock.
The Case for Integrated ML and Mathematical Optimization
So here we have two tools for solving two different but related components of many problems. These tools have their strengths, but they also have their weaknesses. Hopefully, by this point, it is clear that the strengths of these tools can at least in part cancel out the shortcomings of the other.
We discussed the possibility of simulating the randomness of model inputs, in other words, iteratively sampling a set of inputs and re-solving the optimization problem with those inputs. However, what if the model inputs could just be predicted accurately? This is where ML comes into the picture. ML can be used to train models to predict model inputs’ values to feed into the optimization. Once ML models are introduced, this approach becomes much more efficient for operational-level decision-making. It’s a lot faster because you only need to make one accurate prediction and then run the optimization model once to get a recommended set of decisions.
We also discussed the issue with ML not answering the inevitable follow-up questions related to prescribing actions. It is clear that in this case, MO can step in to augment ML outputs. ML predictions can be beneficial and insightful on their own. But many decision problems are more vast than one might think. Leaving decision-makers without recommended decisions limits the impact that data science teams can have in helping their organizations. In other words, decision-makers need more than just “actionable insights”. They need recommended actions, and mathematical optimization can help.
Conclusion
Mosaic Data Science has helped numerous organizations across various industries solve their prediction and decision problems with ML and MO. In many engagements, we have found that these two technologies can be leveraged together to improve how we solve problems for our customers. This value can be seen in both high-level strategic decision-making problems and operational-level decision-making that needs to happen quickly. Our data scientists are uniquely qualified to bridge the gap between machine learning and mathematical optimization due to their wide range of experience in the fields of Data Science, Statistics, Mathematics, and Operations Research.


